What Can ABACUS Do Too? | ABACUS Non-Collinear Magnetic Constraint Method: A Data Generation Engine for Machine Learning Potentials of Magnetic Materials

The machine learning potential method provides a powerful means for high-precision atomic-scale simulations and has profoundly influenced the research paradigm in the materials field. Recently, some magnetic model methods have incorporated magnetic physical quantities such as magnetic moments into machine learning potentials, offering new tools for the study of magnetic materials. However, efficient models rely on accurate data, and currently, the development of magnetic models lacks efficient and accurate data generation tools.

Recently, researchers from the AI for Science Institute (AISI), the Graduate School of the China Academy of Engineering Physics, and their collaborators pre-published an article titled "Integrating Deep-Learning-Based Magnetic Model and Non-Collinear Spin-Constrained Method: Methodology, Implementation and Application" on arXiv [1]. Based on the domestic open-source density functional software ABACUS, the article implemented a constrained density functional method, DeltaSPIN, for arbitrary non-collinear magnetic moments. They trained a magnetic model of the pure iron system using ABACUS + DeePSPIN and accurately simulated the ferromagnetic-paramagnetic transition of the BCC phase.

Research Background

For a long time, first-principles calculations have had difficulty simulating the evolution of magnetic configurations. Although model methods can perform calculations with an applied magnetic field, they share the common problem of insufficient accuracy. In recent years, the combination of machine learning potentials and massive first-principles data has solved many complex problems in the field of non-magnetic materials that were difficult to handle with traditional methods, opening up new possibilities for large-scale simulations of magnetic materials.

Recently, some machine learning potential models have started to consider additional physical quantities such as atomic magnetic moments and magnetic torques based on the original models, enabling effective learning and prediction of material magnetism. However, these models have been plagued by a lack of sufficient magnetic first-principles data during the training process.

Although current mainstream material databases contain massive first-principles data, they are basically non-magnetic or magnetic ground state data. These ground state magnetic data cannot meet the sampling requirements of the additional spin degrees of freedom introduced by magnetic models.

To address the shortage of magnetic data, there is an urgent need for an accurate and efficient tool to generate first-principles data under arbitrary magnetic moment conditions at a relatively low cost.

The constrained density functional method (constrained Density Functional Theory, abbreviated as cDFT) can introduce arbitrary constraint conditions based on the Lagrange multiplier method to calculate first-principles data of arbitrary non-ground states, expanding the application scenarios of first-principles calculations.

Research Results

An efficient non-collinear spin-constrained density functional method (spin constrained Density Functional Theory, hereinafter referred to as spin-cDFT), also known as DeltaSPIN [2], has been implemented in the domestic open-source density functional software ABACUS. The DeltaSPIN method has been realized in a unified framework under the plane wave basis set (PW) and the numerical atomic orbital basis set (LCAO) in ABACUS. The specific calculation process is shown in Figure 1. Based directly on the numerical atomic orbitals of ABACUS, a series of preprocessing steps (truncation, smoothing) are carried out to serve as auxiliary orbitals, and atomic magnetic moments are defined using the orbital projection method. Tests have shown that this definition method ensures the locality of magnetic moments while achieving high accuracy.

First, users can arbitrarily set the target magnetic moment of each atom in the STRU file. Different from the traditional ground state self-consistent field iteration, an inner loop is introduced to implement the Lagrange multiplier method for optimization. The double-layer optimization of the inner and outer loops ensures that the output atomic magnetic moments are consistent with the target magnetic moments. At the same time, the Lagrange multiplier when the magnetic moment constraint is satisfied can be theoretically regarded as the magnetic torque, representing the local magnetic field required to reach the corresponding state.

Figure 1: The calculation flowchart of the DeltaSPIN method implemented in ABACUS.

The DeltaSPIN method in ABACUS can pass strict differential tests of atomic forces, lattice stresses, and magnetic torques under arbitrary non-collinear magnetic configurations (as shown in Figure 2) and is currently undergoing extensive testing.

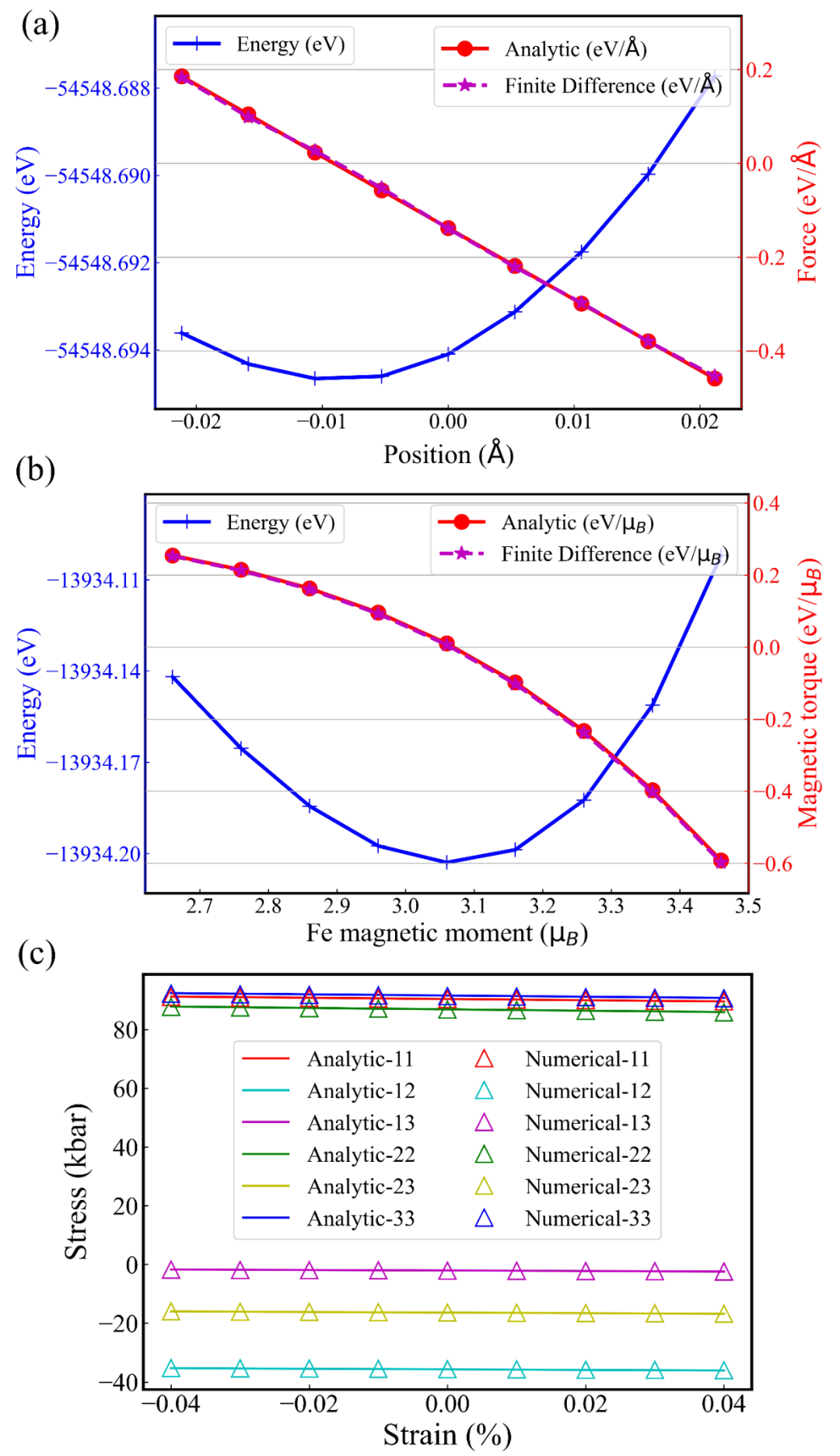
Figure 2: (a) The differential test of atomic forces for BCC-Fe; (b) The differential test of magnetic torques for NiMnTi; (c) The differential test of lattice stresses for FeNi.

ABACUS can efficiently generate non-collinear first-principles data for magnetic models of machine learning potentials. In Figure 3, the first-principles potential energy surfaces of the BCC and FCC phases of elemental iron are shown using the calculation results of DeltaSPIN.

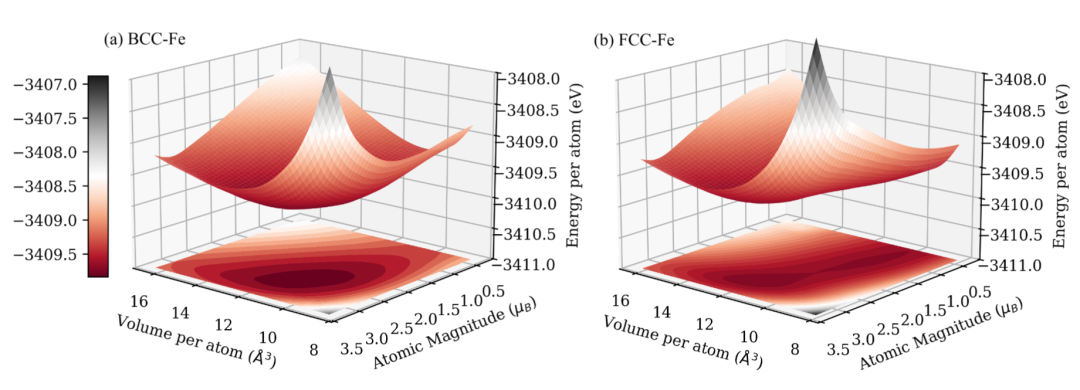
Figure 3: The shapes of the potential energy surfaces of BCC-Fe and FCC-Fe under ferromagnetic configurations at different volumes and magnitudes of magnetic moments, which are calculated by the DeltaSPIN method in ABACUS.

Training and Application of the Iron System Magnetic Model

Iron is the most important magnetic element. The recently proposed DeePSPIN model method [3 - 4] was selected. Based on the first-principles calculations of DeltaSPIN in ABACUS and combined with DPGen active learning, 21,442 sets of first-principles data for pure iron crystals (Fe) with a plane wave basis set and 35,164 sets with a numerical atomic orbital basis set were generated respectively. During sampling, the BCC and FCC phases of iron, as well as their corresponding ferromagnetic, antiferromagnetic, and bilayer antiferromagnetic perturbed configurations, were considered.

Based on the trained DeePSPIN model, Lammps was used for magnetic molecular dynamics simulations. In magnetic molecular dynamics simulations, the control of temperature and pressure can also achieve good results. As shown in Figure 4, during the 0-pressure NPT simulations at 800K and 1200K, after a certain period of equilibrium, the total magnetic moment, temperature, and pressure of the system all show stable trends. During the process of gradually increasing the temperature, the magnetism of BCC-Fe was observed to gradually weaken, and a ferromagnetic-paramagnetic transition occurred at around 1000K. This Curie temperature is very close to the experimentally observed 1043 K (Figure 5,Figure 6).

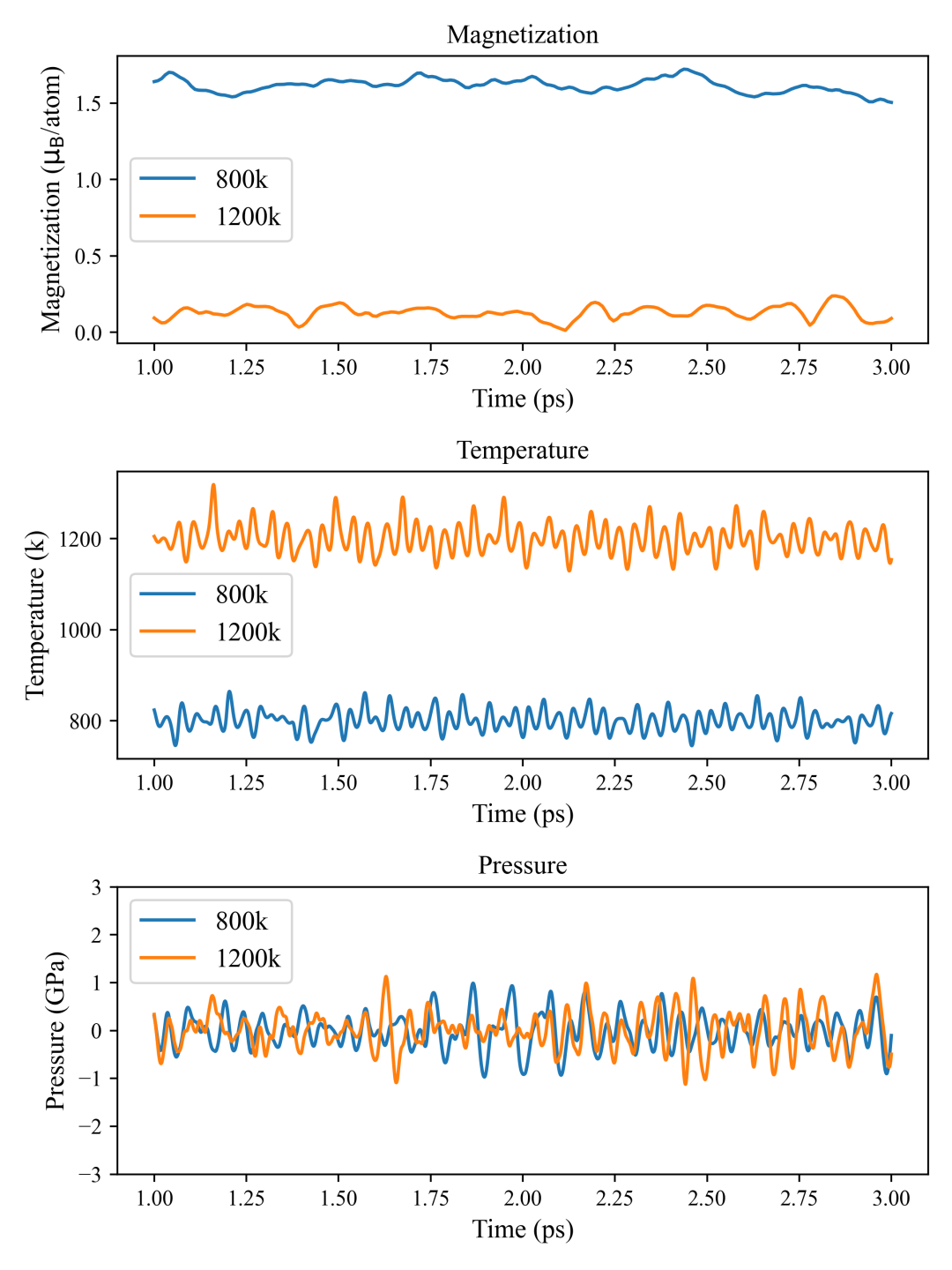
Figure 4: The total magnetic moment, temperature, and pressure of the system after equilibrium in the NPT simulation at 0 pressure and temperatures of 800K and 1200K, using the model trained with numerical atomic orbital data.

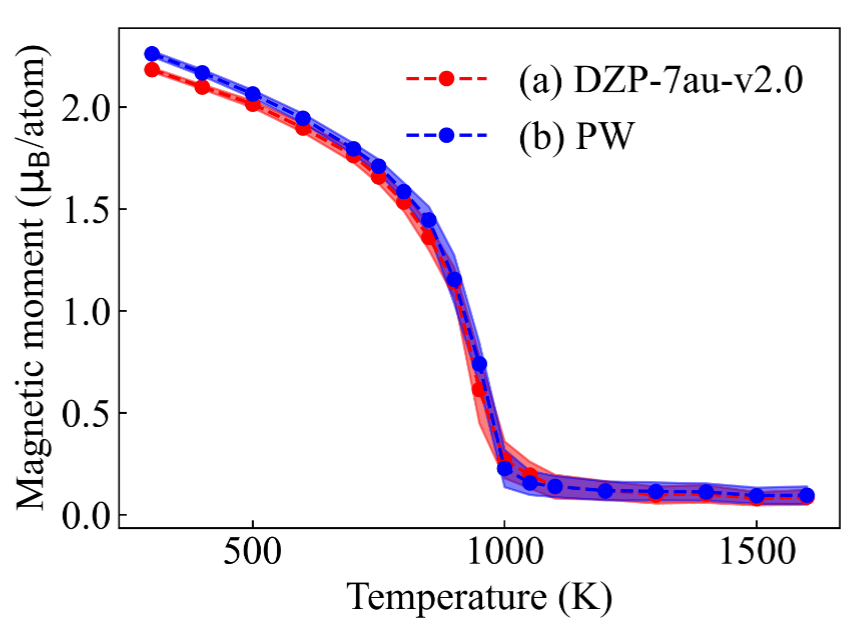
Figure 5: The magnetic changes of the BCC-Fe system at different temperatures in the molecular dynamics simulation of heating up, using the DeePSPIN model trained with the data of the numerical atomic orbital (DZP) basis set in ABACUS (red) or the data of the plane wave basis set (blue). The transition of magnetic order occurs at around 1000K.

Figure 6: The NPT simulation of heating up from 50K to 1200K for 10ps using the model trained with numerical atomic orbital data. The arrows in the figure represent the magnitude and direction of the atomic magnetic moments. Red and blue represent the positive and negative directions of the magnetic moments along the Z-axis respectively. As the temperature rises, the atomic magnetic moments of the system gradually change from the initial ferromagnetic state where all atomic magnetic moments are uniformly oriented in the positive direction of the Z-axis to a paramagnetic state where the magnetic moments are oriented in various directions.

Outlooks

This software is currently the only professional tool globally that can provide training data for magnetic excited states. Combined with DeePSPIN, it will have the ability to perform molecular dynamics simulations of multiple ensembles such as NVE, NVT, and NPT in lattice-spin multi-physics field coupling systems. Currently, its cost on CPUs is already very competitive. The next step is to continue optimizing performance and efficiently support DCU-accelerated computing.

On the other hand, accurate first-principles calculations of magnetic materials remain at the forefront of challenging research directions. The ABACUS development team is conducting extensive tests and plans to introduce a reliable data generation solution for general magnetic material models based on ABACUS in the future.

How to Use

Currently, the development branch of DeltaSPIN in ABACUS is still in internal testing. Cooperation is welcome. Please contact:

Teacher Zheng: zhengdy@aisi.ac.cn

Teacher Xu: bxu@gscaep.ac.cn

References

[1] Integrating Deep-Learning-Based Magnetic Model and Non-Collinear Spin-Constrained Method: Methodology, Implementation and Application, arXiv preprint arXiv:2501.14382

[2] Z. Cai, K. Wang, Y. Xu, S.-H. Wei, and B. Xu, Quantum Front. 2, 21 (2023)

[3] T. Yang, Z. Cai, Z. Huang, W. Tang, R. Shi, A. Godfrey, H. Liu, Y. Lin, C.-W. Nan, M. Ye, L. Zhang, K. Wang, H. Wang, and B. Xu, Phys. Rev. B 110, 064427 (2024)

[4] DeePMD-kit v3: A Multiple-Backend Framework for Machine Learning Potentials, arXiv preprint arXiv:2502.19161