What Can ABACUS Do Too? | ABACUS + DeepH + KPROJ: Unraveling the Electronic Structure of MoSe₂/WSe₂ Moiré Lattices
Recently, the research group led by Mingxing Chen from the College of Physics and Electronic Science at Hunan Normal University investigated the evolution of flat bands in the MoSe₂/WSe₂ moiré lattices of transition metal dichalcogenides using deep learning potential and Hamiltonian models. In this study, they employed the domestic first-principles software ABACUS, which is based on the linear combination of atomic orbitals (LCAO) basis set, to prepare machine learning datasets. Subsequently, they used DeepH, based on E3 equivariant graph neural networks, to train machine learning models for predicting the moiré lattice Hamiltonian. Diagonalizing the machine learning Hamiltonian yielded the electronic structure of the moiré system. Thereafter, they utilized the self-developed band unfolding program KPROJ to project the wavefunctions of the moiré supercell onto the k-points of the primitive cell and obtained the unfolded band structure, which was used to study the influence of the twist angle on the band structure of transition metal dichalcogenides. This work revealed that the flat bands originating from the valence band edge can stem from the Γ and K valleys. When the H-stacked MoSe₂/WSe₂ moiré lattice has a twist angle of 3.89˚ and spin-orbit coupling (SOC) is not considered, a flat band with a bandwidth of approximately 5 meV appears below the valence band edge at the K point. Subsequently, as the twist angle decreases, this flat band rapidly shifts upward and becomes approximately 20 meV higher than the valence band at the K point. When the twist angle further decreases to 1.7˚, multiple flat bands emerge. The research found that spin-orbit coupling leads to a large spin splitting, comparable to that in the untwisted system (approximately 0.45 eV), and is almost independent of twisting and stacking. Therefore, in the presence of spin-orbit coupling, the flat band in the K valley remains at the top of the valence band. The band unfolding results indicate that the flat bands formed by the Γ valley and the K valley exhibit distinct responses to the twist angle. The Γ valley flat band is highly sensitive to the interlayer coupling and thus rapidly shifts upward as the twist angle decreases. Conversely, the K valley flat band has a weaker dependence on the interlayer coupling and is primarily affected by structural reconstruction. Hence, a relatively small angle (2.13˚) is required to generate the K valley flat band. As the twist angle decreases, this flat band transforms from a honeycomb lattice to a triangular lattice. The relevant research, titled "Evolution of flat bands in MoSe₂/WSe₂ moiré lattices: A study combining machine learning and band unfolding methods", was published in Physical Review B [Phys. Rev. B 110, 235410 (2024)]. Doctoral students Shengguo Yang and Jiaxin Chen are the first and second authors respectively, and Mingxing Chen is the corresponding author.
Research Background
Moiré lattices have become ideal quantum simulation platforms for exploring new physics due to the fact that the electronic flat bands within them can induce numerous novel physical phenomena and effects and are modulated by the twist angle. However, the large size of such systems poses a significant challenge to existing first-principles methods for calculating their electronic structures, making it difficult to understand the evolution of electronic flat bands and related electronic properties. Although first-principles calculations have been conducted on the twisted bilayer transition metal dichalcogenide (tbTMD) systems with twist angles as small as 1.54˚ [1], the first-principles calculations are extremely time-consuming because this type of lattice usually contains a large number of atoms (8322 atoms). Recently, deep learning methods such as deep potential molecular dynamics (DeePMD) [2,3,4] and deep learning DFT Hamiltonian (DeepH) [5,6] have demonstrated that machine learning methods can efficiently and accurately simulate the structures and energy bands of large-scale systems. Applying these methods to twisted systems will contribute to understanding the influence of twisting on the electronic properties of two-dimensional materials. Nevertheless, due to the use of large supercells in such calculations, band folding occurs in the band structure, which may obscure some essential characteristics of the flat bands. Especially for tbTMD, the Γ and K valley flat bands may be mixed in the band structure calculated from the supercell, thus making it difficult to understand the origin and evolution of the flat bands.
In addition, recent scanning tunneling microscope experiments have shown that the H-stacked MoSe₂/WSe₂ moiré system exhibits a deep moiré potential exceeding 300 meV in the valence band [7], and the moiré potential shows a monotonic behavior with the change of the moiré stripe period. As its size increases from 6 nm (3.15˚) to 17 nm (1.08˚), new flat band signals appear at the HMX sites. However, the valley origin remains to be explored.
Research Methods
In this work, a high-quality DP model trained for MoSe₂/WSe₂ was used to perform structural relaxation on the rigid moiré lattice. Subsequently, ABACUS was employed to generate high-precision datasets required by DeepH and conduct graph neural network training. The obtained high-quality DeepH model was used for band structure calculations. Finally, the KPROJ program was used to obtain the unfolded band structure. The calculation flow chart is shown in Figure 1.
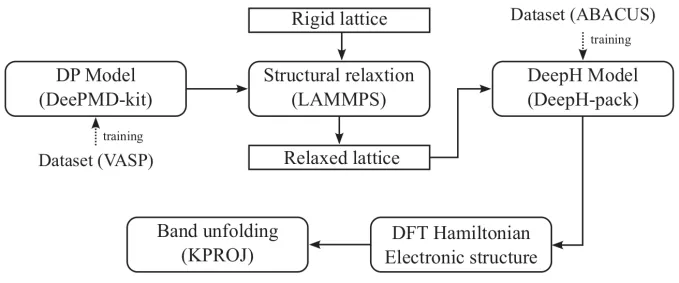
Figure 1 Flowchart of the calculation scheme
Research Results
This work studied the twisted bilayer MoSe₂/WSe₂ with twist angles ranging from 21.79˚ to 1.7˚. The results revealed that the structural reconstruction of the moiré stripes increases as the twist angle decreases. During this process, the interlayer distances of the locally high-symmetry configurations in the moiré lattice also change accordingly. Specifically (for H stacking), the interlayer distances of HMX and HMM decrease as the twist angle becomes smaller, while the interlayer distance of HXX changes in the opposite way.
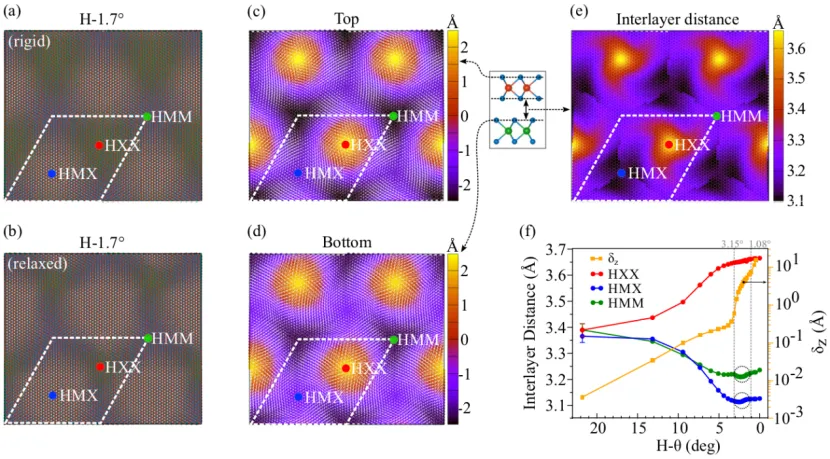
Figure 2 Structural reconstruction and local interlayer distances in the MoSe₂/WSe₂ moiré lattice
In tbTMD, the Γ valley is mainly composed of pz and dz² orbitals with an out-of-plane orientation, while the K valley is primarily composed of px/py and dxy/dx² - y² orbitals with an in-plane orientation. This characteristic endows the Γ valley with significant interlayer hybridization, while the K valley is less affected by interlayer hybridization. Since the interlayer coupling strengthens as the twist angle decreases, during the process of decreasing the twist angle, the Γ valley flat band rapidly moves upward and exceeds the valence band top of the K valley (the K valley band is hardly affected) at approximately 3.15˚. As the twist angle decreases to 2.13˚, the K valley flat band forms. When the twist angle is further decreased to 1.7˚, multiple Γ valley flat bands and K valley bands form, and the two types of flat bands become difficult to distinguish.
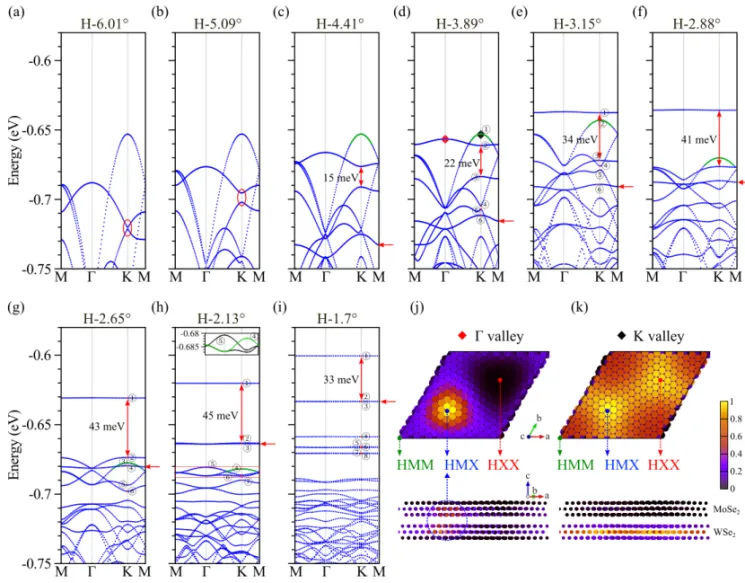
Figure 3 Band structure as a function of the twist angle
The band unfolding technique can assist in determining which valley these flat bands originate from. The following band unfolding results clearly reveal the formation and evolution of the Γ and K valley flat bands. It can be seen that the Γ valley is lower than the K valley in the moiré lattice at 4.41˚. As the twist angle decreases to 3.15˚, the Γ valley flat band gradually becomes higher than the K valley. As the twist angle decreases, multiple Γ valley flat bands are generated and become higher than the valence band top at the K point, while the K valley flat band only forms after the twist angle reaches 2.13˚.
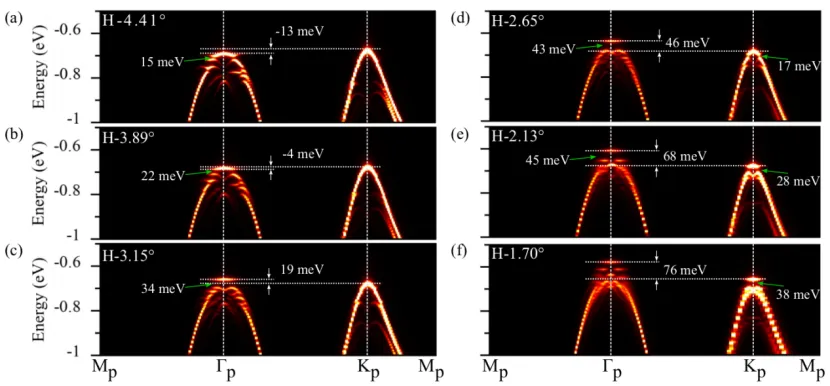
Figure 4 Unfolded band structure
Wavefunction analysis revealed the modulation of the Γ and K valley flat bands by the moiré periodic potential. At 3.89˚, the Γ flat band has already formed, and its wavefunction is mainly localized at the HMX sites (band 2). The wavefunction of the K valley band is mainly localized at the WSe₂ of the HMX and HXX sites (band 1), and the wavefunction distribution at this time appears as a honeycomb lattice. As the twist angle decreases to 1.7˚, the wavefunction of the Γ valley flat band becomes more localized and maintains its pattern unchanged (it then becomes band 1 at 3.15°). With the formation of the K valley flat band, its corresponding wavefunction distribution transforms from a honeycomb lattice to a triangular lattice and becomes localized (as indicated by the green arrow).
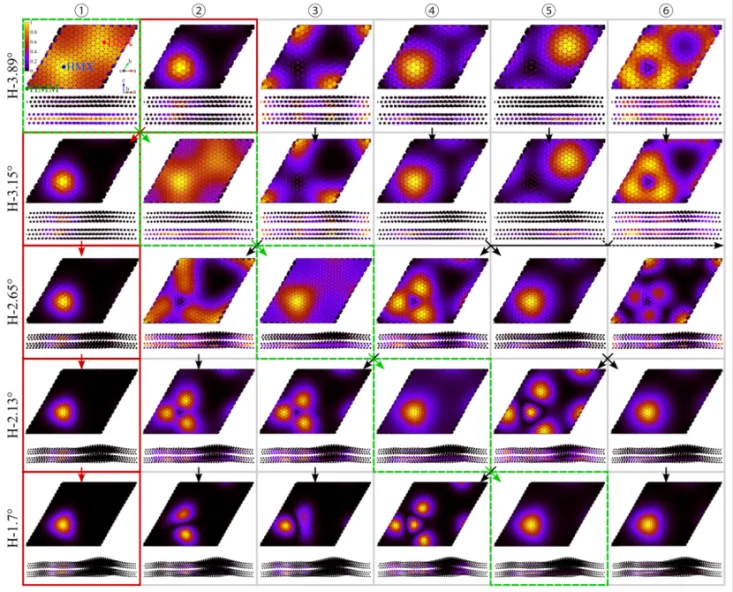
Figure 5 Distribution of the wavefunctions of the six highest valence bands at the K point. The serial numbers represent energy levels (see Figure 3)
Summary
This paper combined machine learning methods and the band unfolding technique to study the electronic structure of the MoSe₂/WSe₂ moiré lattice, enabling the tracking of the evolution of flat bands with the twist angle. The results showed that when the twist angle decreases to 2.13˚, multiple flat bands emerge. Since the Γ valley flat band is affected by both interlayer coupling and structural reconstruction, while the K valley flat band is mainly modulated by structural reconstruction, the twist angle required for the appearance of the Γ valley flat band is much larger than that for the K valley flat band, and the Γ valley flat band moves to higher energy levels much faster than the K valley flat band. By analyzing the wavefunction characteristics of the valence band at K, this study found that the K valley flat band undergoes a transformation from a hexagonal to a triangular lattice. The researchers further discussed the influence of spin-orbit coupling (SOC) on the flat bands of the MoSe₂/WSe₂ moiré lattice. The results showed that, similar to the untwisted TMD bilayer, SOC has little effect on the Γ valley flat band but leads to significant splitting in the K valley. After considering SOC, the energy level of the K valley flat band will be higher than that of the Γ valley flat band, that is, the K valley flat band becomes the top of the valence band of the MoSe₂/WSe₂ moiré lattice.
References
[1] Naik M. H., Kundu S., Maity I., Jain M., Origin and evolution of ultraflat bands in twisted bilayer transition metal dichalcogenides: Realization of triangular quantum dots, Phys. Rev. B 102, 075413 (2020).
[2] Zhang L., Han J., Wang H., Car R., E W., Deep potential molecular dynamics: A scalable model with the accuracy of quantum mechanics, Phys. Rev. Lett. 120, 143001 (2018).
[3] Wang H., Zhang L., Han J., E W., DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics, Comput. Phys. Commun. 228, 178 (2018).
[4] Zeng J., Zhang D., Lu D., Mo P., Li Z., Chen Y., Rynik M., Huang L., Li Z., Shi S., Wang Y., Ye H., Tuo P., Yang J., Ding Y., Li Y., Tisi D., Zeng Q., Bao H., Xia Y. et al., DeePMD-kit v2: A software package for deep potential models, J. Chem. Phys. 159, 054801 (2023).
[5] Li H., Wang Z., Zou N., Ye M., Xu R., Gong X., Duan W., Xu Y., Deep-learning density functional theory Hamiltonian for efficient ab initio electronic-structure calculation, Nat. Comput. Sci. 2, 367 (2022).
[6] Gong X., Li H., Zou N., Xu R., Duan W., Xu Y., General framework for E(3)-equivariant neural network representation of density functional theory Hamiltonian, Nat. Commun. 14, 2848 (2023).
[7] Shabani S., Halbertal D., Wu W., Chen M., Liu S., Hone J., Yao W., Basov D. N., Zhu X., Pasupathy A. N., Deep moiré potentials in twisted transition metal dichalcogenide bilayers, Nat. Phys. 17, 720 (2021).