What Can ABACUS Do Too? | Accelerating Hybrid Functional Calculations with Numerical Atomic Orbital Basis Sets Using Space-Group Symmetry
Hybrid functionals (HDFs) overcome the shortcomings of local/semi-local functionals—such as the underestimation of band gaps—by incorporating exact exchange (EXX), but this comes at the cost of high computational expense. ABACUS combined with LibRI enables linear-scaling calculations of hybrid functionals, and on this basis, applying space-group symmetry can further reduce the computational load.
Prior to version 3.8.0, ABACUS already supported symmetry acceleration for local/semi-local functionals: it reduces the number of Kohn-Sham (KS) equations to be solved by reducing k-points to the irreducible Brillouin zone (IBZ). However, due to the lack of implementation for space-group transformations of the density matrix, symmetry acceleration was not supported for cases involving non-local Hamiltonians (e.g., hybrid functionals). On the other hand, symmetry reduction can also be applied to real-space two-electron integrals (ERIs) for the EXX term. Nevertheless, currently available software (such as CRYSTAL and Turbomole) only implements this for algorithms that directly compute four-center integrals, without further accelerating symmetry application based on the resolution of the identity (RI) method—a common approach to speed up ERI calculations.
Recently, researchers from the Institute of Physics, Chinese Academy of Sciences, and Peking University used symmetry to accelerate two key steps in hybrid functional calculations with ABACUS+LibRI: they not only reduced the time required for diagonalization to solve the Kohn-Sham equations by means of k-point reduction, but also reduced the real-space region using symmetry. This further accelerated the calculation of the real-space EXX Hamiltonian by several times, building on the linear scaling achieved by the local resolution of the identity (LRI) method [1]. This feature is supported in ABACUS v3.8.0, LibRI v0.2.0, and later versions.
The related work, titled “Applying Space-Group Symmetry to Speed Up Hybrid-Functional Calculations within the Framework of Numerical Atomic Orbitals”, was published in the Journal of Chemical Theory and Computation: https://pubs.acs.org/doi/10.1021/acs.jctc.5c00537 [2].
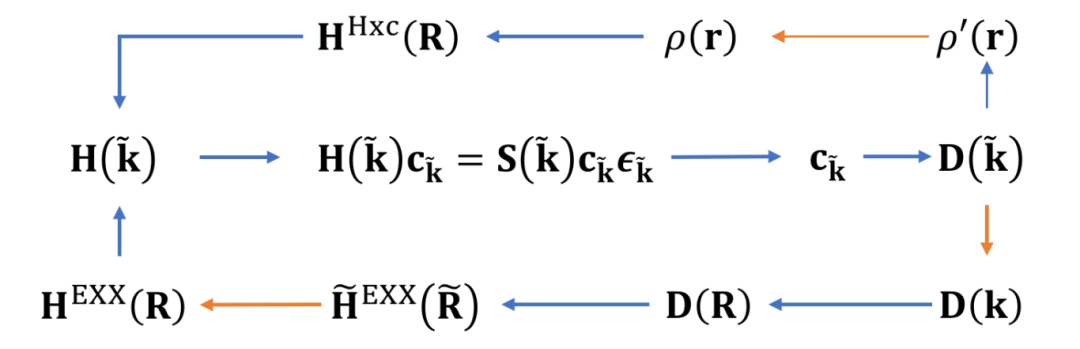
Figure 1: KSDFT workflow for hybrid functionals, where orange arrows indicate steps involving the application of symmetry.
Research Methods
For numerical atomic orbital basis sets, the transformation formulas of the k-space density matrix and real-space Hamiltonian under the space-group operation 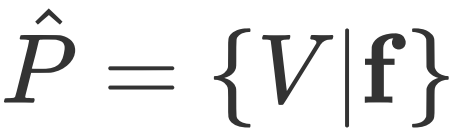 are:
are:
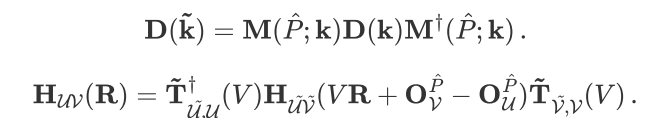
Here, T and M are the rotation matrices of symmetry operations in the atomic orbital and Bloch orbital representations, respectively, which can be derived using Wigner D-matrices (see the original paper [2] for details). After applying symmetry, only the EXX Hamiltonian for atomic pairs in the irreducible region needs to be computed in real space:
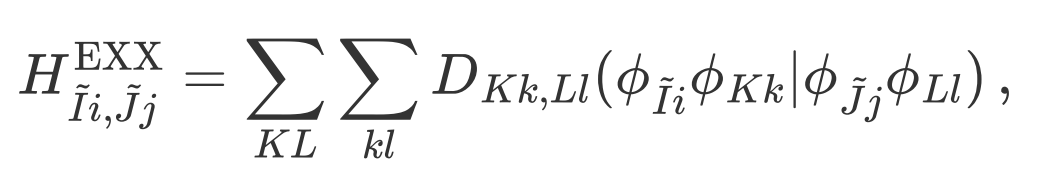
The formula for converting four-center integrals to two-center integrals using the local resolution of the identity (LRI) method is:
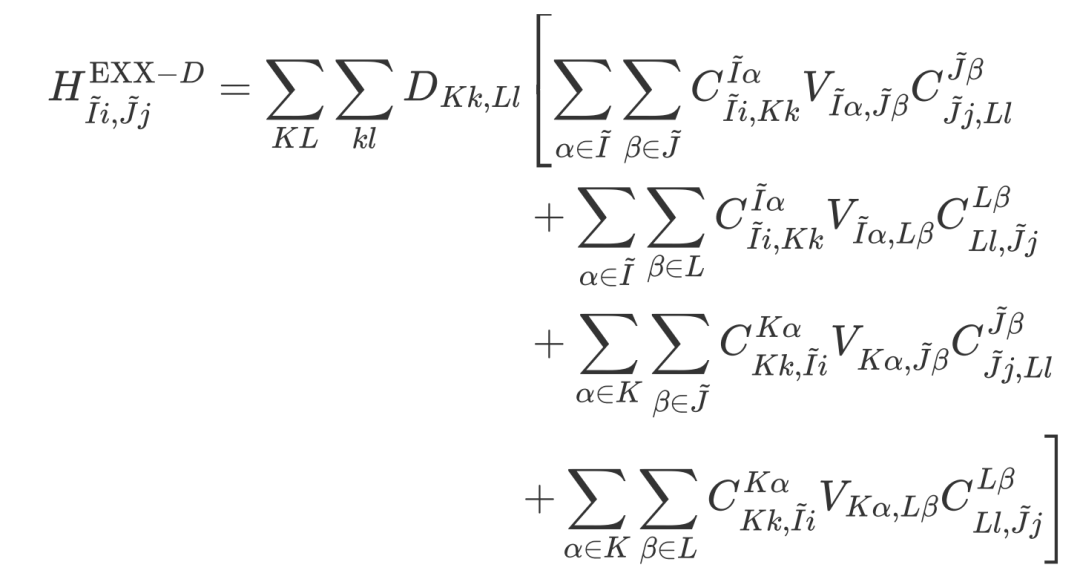
Where C is the coefficient for expanding atomic orbital products using auxiliary basis sets, and V is the Coulomb matrix in the auxiliary basis representation.
To reduce the redundancy of tensors across processes and save memory, LibRI computes the EXX Hamiltonian by switching from the "D perspective" to the "V perspective" [1] (as shown in Figure 2). However, when using symmetry to reduce the real-space region, this perspective switch causes the four types of terms computed simultaneously to contribute to different irreducible atomic pairs, introducing additional difficulties in screening the irreducible real-space region during code implementation.
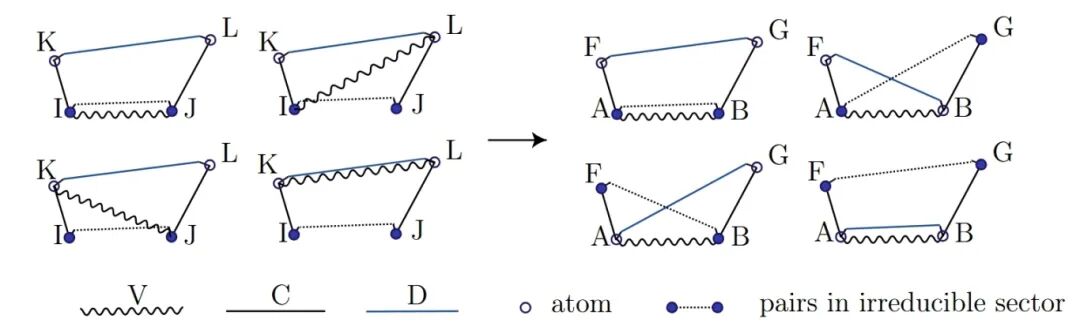
Figure 2: When switching the Hamiltonian grouping method from the D perspective to the V perspective, irreducible atomic pairs of the four term types appear at different positions.
LibRI v0.2.0 [3] has improved the underlying algorithm by reducing four nested loops to three, which reduces the computation time by an order of magnitude while resolving this difficulty: the new algorithm uniformly iterates over atoms in the irreducible region in the outermost loop and the second innermost loop when computing all types of terms.
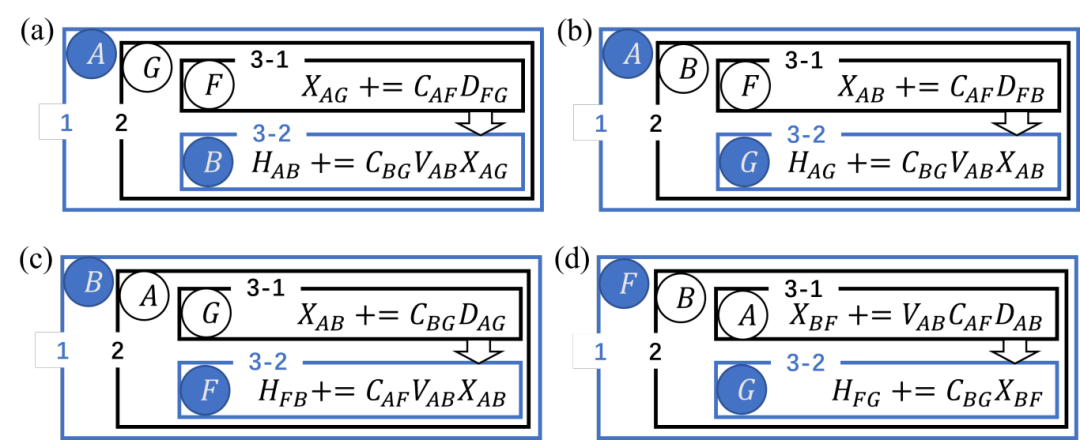
Figure 3: Schematic diagram of EXX Hamiltonian calculation with real-space irreducible region screening based on the new "loop3" algorithm in LibRI v0.2.0, where blue circles represent irreducible atomic pairs.
Results
We tested systems with various symmetries (see Table 1). The results show that:
- The acceleration ratio for diagonalization is consistent with the k-point reduction factor and increases with the increase in k-point density.
- The acceleration ratio for calculating the real-space EXX Hamiltonian varies by system:
- For 3D uniform k-point sampling: The acceleration ratio first increases and then decreases as k-points are densified. Due to the higher symmetry of the BvK supercell for odd k-points, the acceleration ratio for odd k-points is higher than that for even k-points (as shown in Figure 4).
- For 2D uniform k-point sampling: The acceleration ratio first increases with the increase in k-points and then stabilizes, with no significant fluctuation between odd and even k-points (as shown in Figure 5).
Figure 6 compares the acceleration ratios of four similar structures with different symmetries. The highest symmetry (Oh) can accelerate the calculation of the real-space EXX Hamiltonian by 4–5 times.
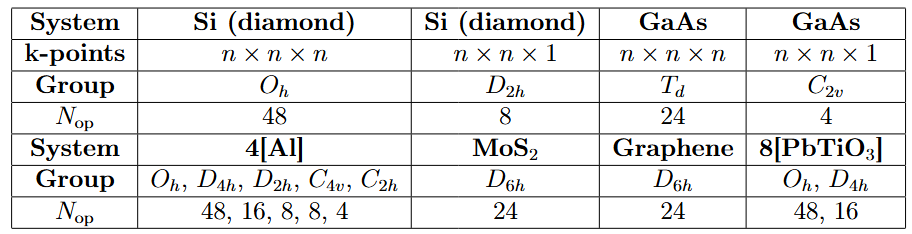
Table 1: Symmetry (Point Groups of Space Groups) and Number of Operations for Tested Systems
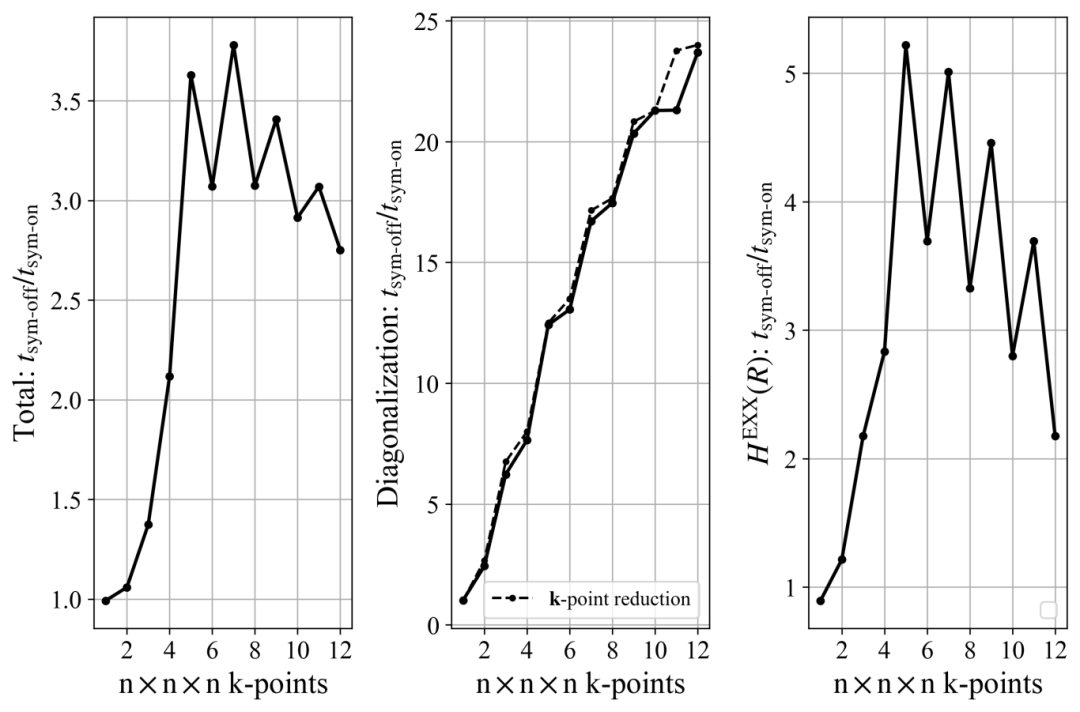
Figure 4: HSE functional calculations for crystalline silicon (Oh group), showing the variation of the overall acceleration ratio, k-space diagonalization acceleration ratio, and real-space exact exchange potential acceleration ratio with 3D uniform k-point sampling density.
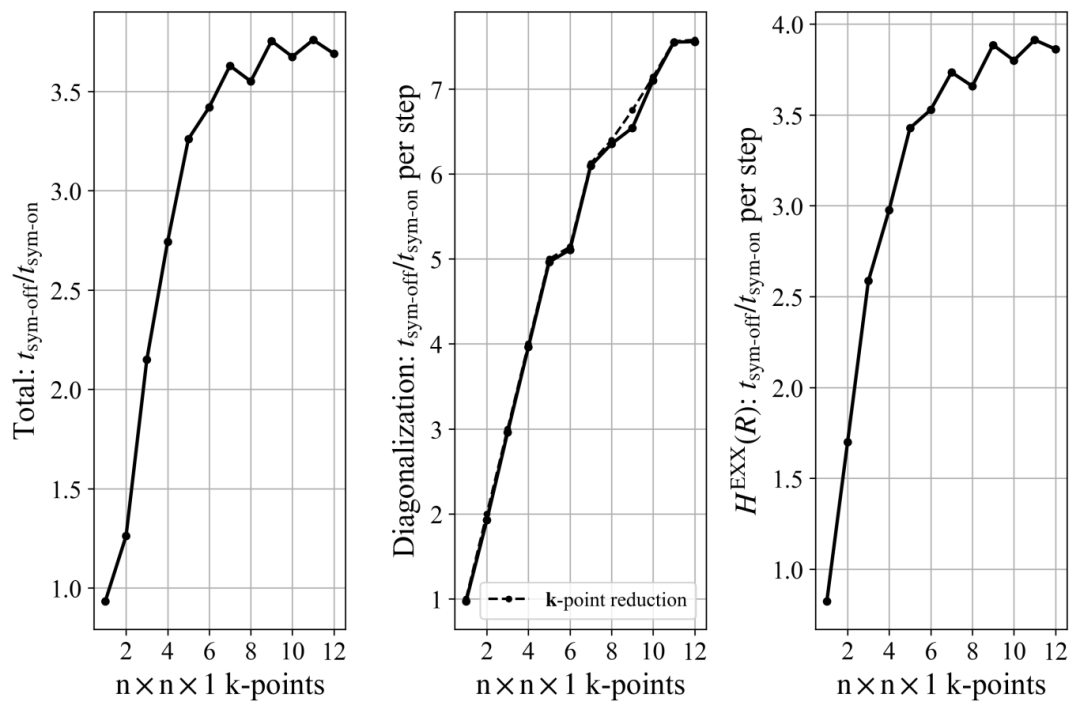
Figure 5: HSE functional calculations for MoS₂ crystals (D6h group), showing the variation of the overall acceleration ratio, k-space diagonalization acceleration ratio, and real-space exact exchange potential acceleration ratio with 2D uniform k-point sampling density.
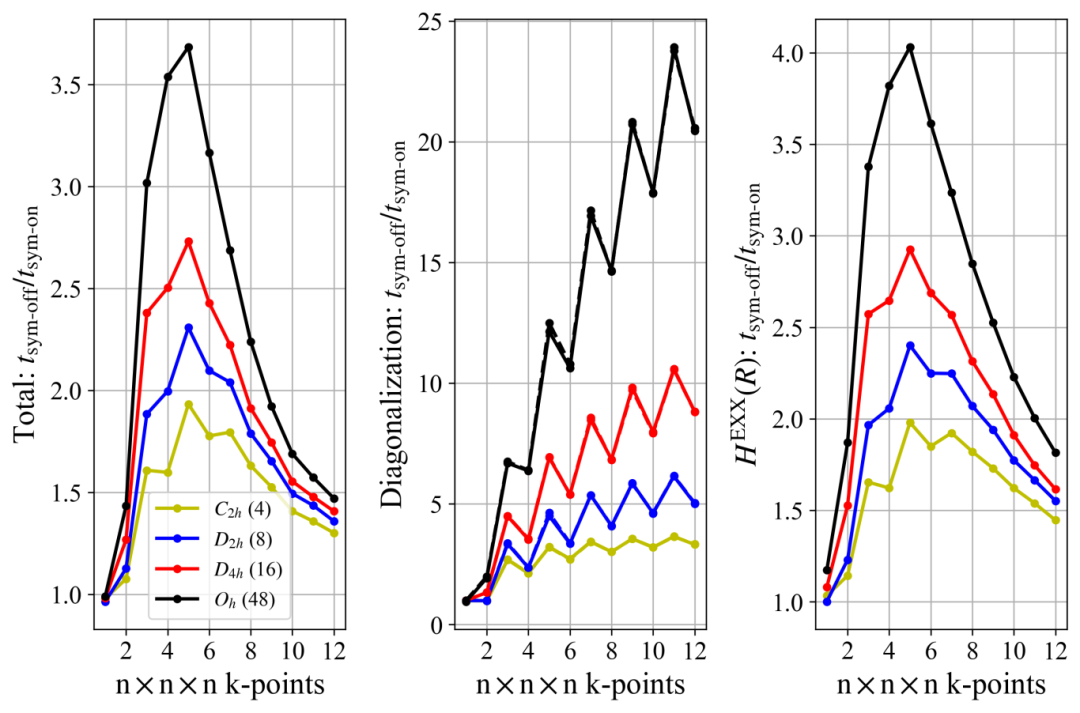
Figure 6: Acceleration ratios for HSE calculations of 4-atom Al supercells with four types of symmetry.
Conclusion
By leveraging the transformation relationships of the density matrix and Hamiltonian under symmetry operations for numerical atomic orbital basis sets, the researchers restricted k-space and real-space calculations to irreducible regions. This significantly accelerated two major time-consuming bottlenecks in the ABACUS+LibRI hybrid functional calculation workflow: "diagonalization to solve the Kohn-Sham equations" and "calculation of the exact exchange Hamiltonian".
Notably, symmetry acceleration in real space was achieved for the first time on the basis of the linear-scaling acceleration of the LRI method. Furthermore, relying on LibRI's general program framework, this approach can be extended to methods beyond density functional theory, such as the GW method.
References
[1] Peize Lin, Xinguo Ren, and Lixin He. Journal of Chemical Theory and Computation 2021, 17 (1), 222–239, DOI: 10.1021/acs.jctc.0c00960 (https://pubs.acs.org/doi/10.1021/acs.jctc.0c00960)
[2] Yu Cao, Min-Ye Zhang, Peize Lin, Mohan Chen, and Xinguo Ren. Journal of Chemical Theory and Computation 2025, 21 (16), 8086–8105, DOI: 10.1021/acs.jctc.5c00537 (https://pubs.acs.org/doi/10.1021/acs.jctc.5c00537)
[3] https://github.com/abacusmodeling/LibRI