What Can DP Do too? | DeePMD Helps Reveal the Phase-Transformation-Induced Plasticity Mechanism in Zirconia Shape Memory Ceramics
The research group led by David Rodney from the University of Lyon 1 collaborated with Fuzhi Dai (now a distinguished professor at the University of Science and Technology Beijing) from the Beijing Institute for Scientific Intelligence. They developed a high-precision deep neural network potential function model based on the DeePMD-kit software. This model reveals the complex phase-transformation-induced plasticity (TRIP) mechanism in ceria (CeO₂)-doped zirconia (ZrO₂) ceramics. The related results were published in the authoritative journal Acta Materialia in materials science under the title "Transformation-induced plasticity in CeO₂-ZrO₂ ceramics: Atomic-scale insights using a deep neural network potential" (https://doi.org/10.1016/j.actamat.2024.120661). The model and dataset have been made public on the AIS-Square platform for researchers to use: https://www.aissquare.com/models?search=CeO₂-ZrO₂. The first author of this paper is Jinyu Zhang (now a postdoctoral fellow at Osaka University), and the corresponding author is David Rodney.
Research Background
ZrO₂ ceramics have attracted much attention due to their excellent mechanical properties, such as phase-transformation-induced plasticity (TRIP), shape memory effect, and superelasticity. However, the complex atomic-scale mechanisms behind these phenomena still need to be systematically studied. ZrO₂ ceramics exhibit excellent plasticity through the phase transformation from the tetragonal phase to the monoclinic phase. This phase transformation is usually accompanied by volume expansion and shear deformation, significantly improving the toughness of the material. However, although the traditional view considers this phase transformation process to be simple and straightforward, the latest research suggests that there may be intermediate phases, and these intermediate processes may change the mechanical response of the TRIP effect. For example, in previous micropillar experiments [1], it was observed that when compressed along the tetragonal ⟨110⟩ direction (the crystallographic indices of the tetragonal phase are defined in a double cell), although there is a large shear stress, the corresponding phase transformation mode cannot be activated, and the plasticity is poor. In addition, the experiment observed richer TRIP deformation modes in polycrystalline compression deformation than in single crystals. The mechanisms behind these phenomena need to be explored.
Method Introduction
The research team utilized the active learning and transfer learning functions of the DP-GEN software to efficiently construct a CeO₂-ZrO₂ dataset based on the PBEsol and SCAN+rVV10 functionals on the basis of the previous DFT dataset of pure ZrO₂ [2]. Then, they used the DeePMD-kit software to train and generate a deep neural network potential function model. This model can not only accurately describe the basic properties (such as lattice constants and elastic moduli) of various phases of ZrO₂ and cubic CeO₂ but also quantitatively reproduce the experimentally obtained pressure-temperature phase diagram of ZrO₂ (Figure 1) and the tetragonal-monoclinic phase transformation properties of the CeO₂-doped ZrO₂ system, including the changes in phase transformation temperature and latent heat with composition (Figure 2).
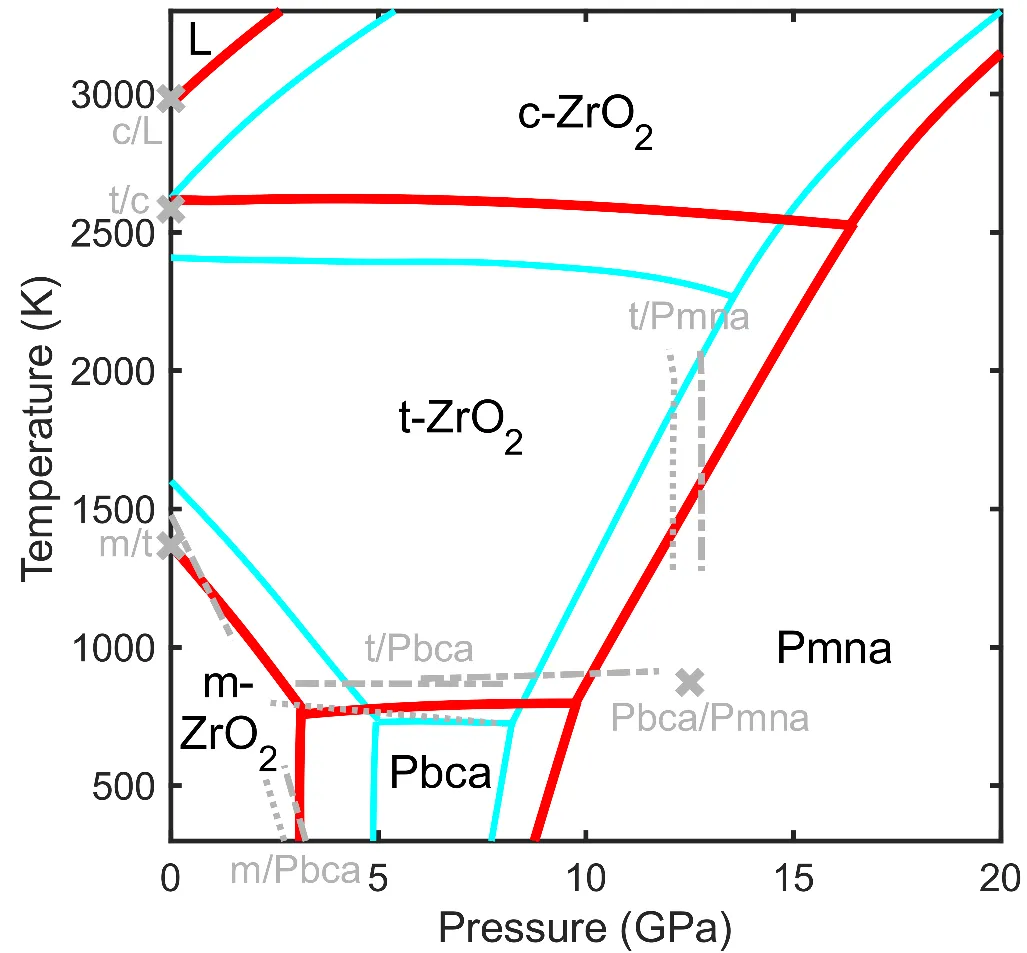
Figure1: Pressure - temperature phase diagram of pure ZrO₂. The red and blue lines are the simulation results of the potential function trained with the SCAN+rVV10 dataset (this work) and the potential function trained with the PBEsol dataset [2], respectively. The gray markers are the previous experimental data.
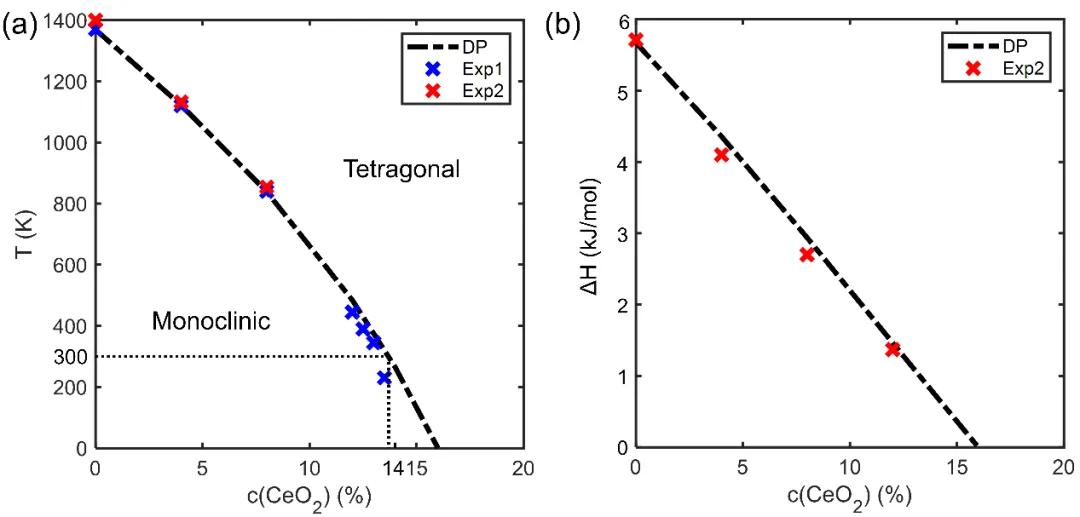
Figure2: Thermodynamic properties of the tetragonal - monoclinic phase transformation in the CeO₂-ZrO₂ system. The dashed lines are the simulation results, and the data points are the previous experimental data. (a) Variation of the phase transformation temperature and (b) variation of the latent heat of phase transformation with composition.
Results and Discussion
TRIP Effect in Polycrystalline Tetragonal Zirconia
The research team simulated the deformation process of a quasi-two-dimensional polycrystal of tetragonal CeO₂-ZrO₂ under uniaxial compression (in the vertical direction) (as shown in Figure 3). During the loading process, the grains with the [001] axis orientation first undergo a ferroelastic transformation, while the grains with the [101] orientation (the crystallographic indices of the tetragonal phase are defined in a double cell) preferentially undergo a tetragonal-monoclinic martensitic phase transformation through the C correspondence. These martensitic phases can cross the grain boundaries and enter adjacent grains with poor orientation, inducing an autocatalytic martensitic phase transformation. After unloading, the martensitic phase undergoes a reverse transformation to achieve superelastic recovery, while the ferroelastic transformation is retained. The research team also further studied the deformation process of a three-dimensional polycrystal (a nearly one-million-atom simulation for 5 nanoseconds, Figure 4) under uniaxial compression and observed that under complex stresses, the tetragonal grains can achieve multiple phase transformation paths and richer deformation modes.

Figure3: Microstructural evolution process of 14%CeO₂-ZrO₂ quasi - two - dimensional polycrystal under uniaxial compression at 300K. Different colors represent different variants of the tetragonal and monoclinic phases.
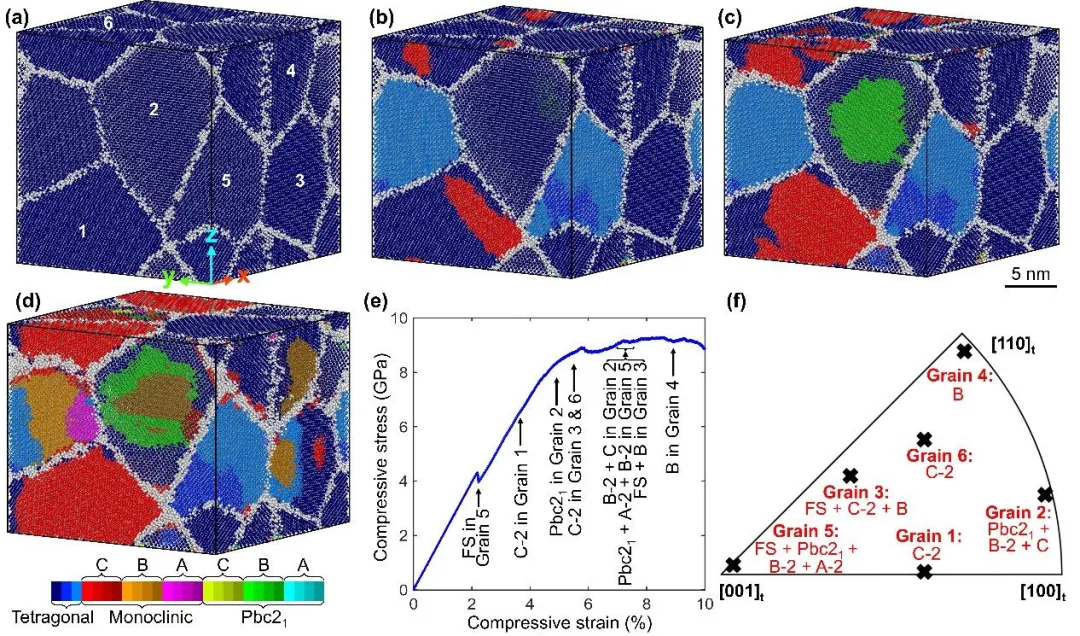
Figure4: Phase - transformation - induced plasticity in a three - dimensional polycrystal achieved by uniaxial compression at 300K. Solid - state phase transformations or ferroelastic transformations that occur when the compressive strain is (a) ε = 0.0%, (b) ε = 5.1%, (c) ε = 6.8%, (d) ε = 9.7%; (e) Corresponding stress - strain curves, with solid - state phase transformation or ferroelastic transformation events marked; (f) Types of solid - state phase transformations or ferroelastic transformations in six grains of the polycrystal, and the orientation of the compression direction relative to the initial tetragonal grains is shown in the stereographic projection.
Tensile-Compressive Asymmetry in the ⟨110⟩ Direction of Single-Crystal Tetragonal Zirconia
Geometric calculations show that under uniaxial deformation in the tetragonal ⟨110⟩ direction, the phase transformation mode of the B correspondence has a large shear stress, but the TRIP phenomenon was not observed in the corresponding micropillar compression experiment [1]. Our simulations (Figure 5) show that the phase transformation mode of the B correspondence requires a ferroelastic transformation. Under uniaxial loading in the ⟨110⟩ direction, the potential barrier of the martensitic transformation always decreases; however, during compression in the ⟨110⟩ direction, the potential barrier of the ferroelastic transformation continuously increases, hindering the activation of the martensitic phase transformation; while during tension in the ⟨110⟩ direction, the potential barrier of the ferroelastic transformation decreases, enabling the phase transformation of the B correspondence to occur. The simulation results of micropillar deformation verify this phenomenon (Figure 6) and reveal the importance of this intermediate state in activating the TRIP mode. The ferroelastic transformation of the intermediate state leads to strong tensile-compressive asymmetry, making it impossible to predict the activation of the deformation mode solely based on the shear stress. This phenomenon has implications for the study of the mechanical responses of other deformation processes with intermediate states (such as some twinning deformations in metastable β-titanium alloys and NiTi alloys).
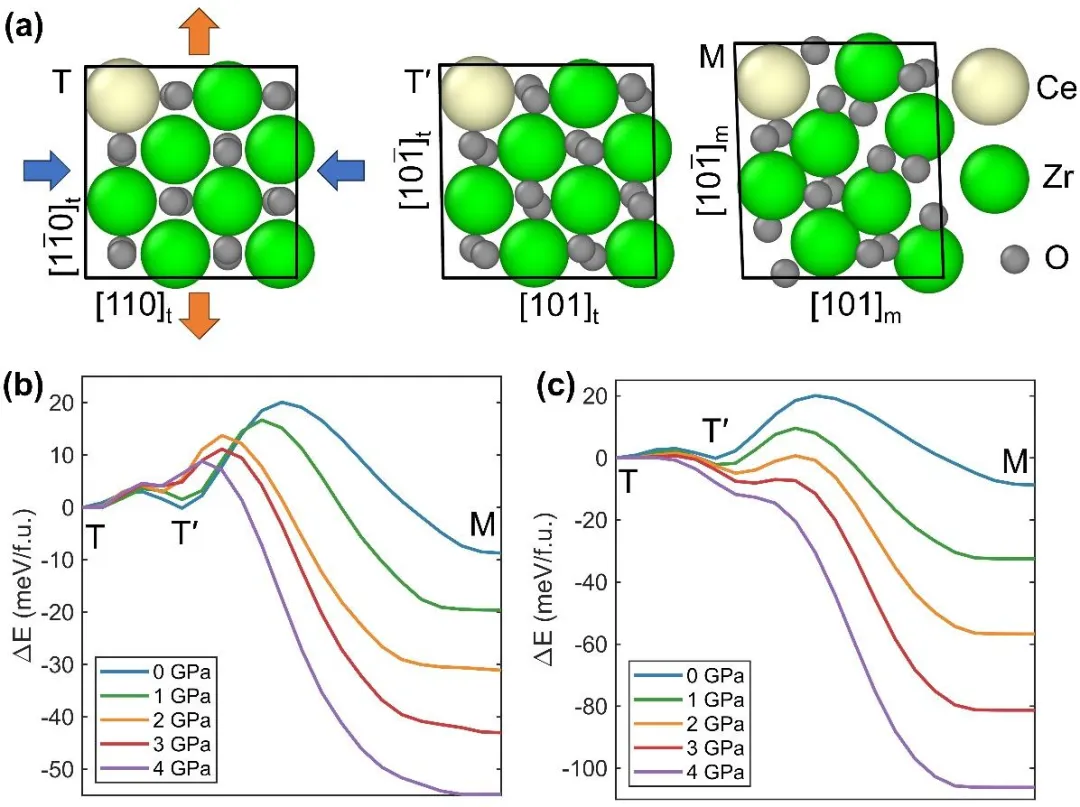
Figure5: Variation of the phase transformation barrier with uniaxial loading in the ⟨110⟩ direction under the phase transformation mode of the B correspondence. (a) Configurations of key nodes on the phase transformation path, with arrows indicating the direction of compression or tension; (b) Different compressive stresses; (c) Different tensile stresses.
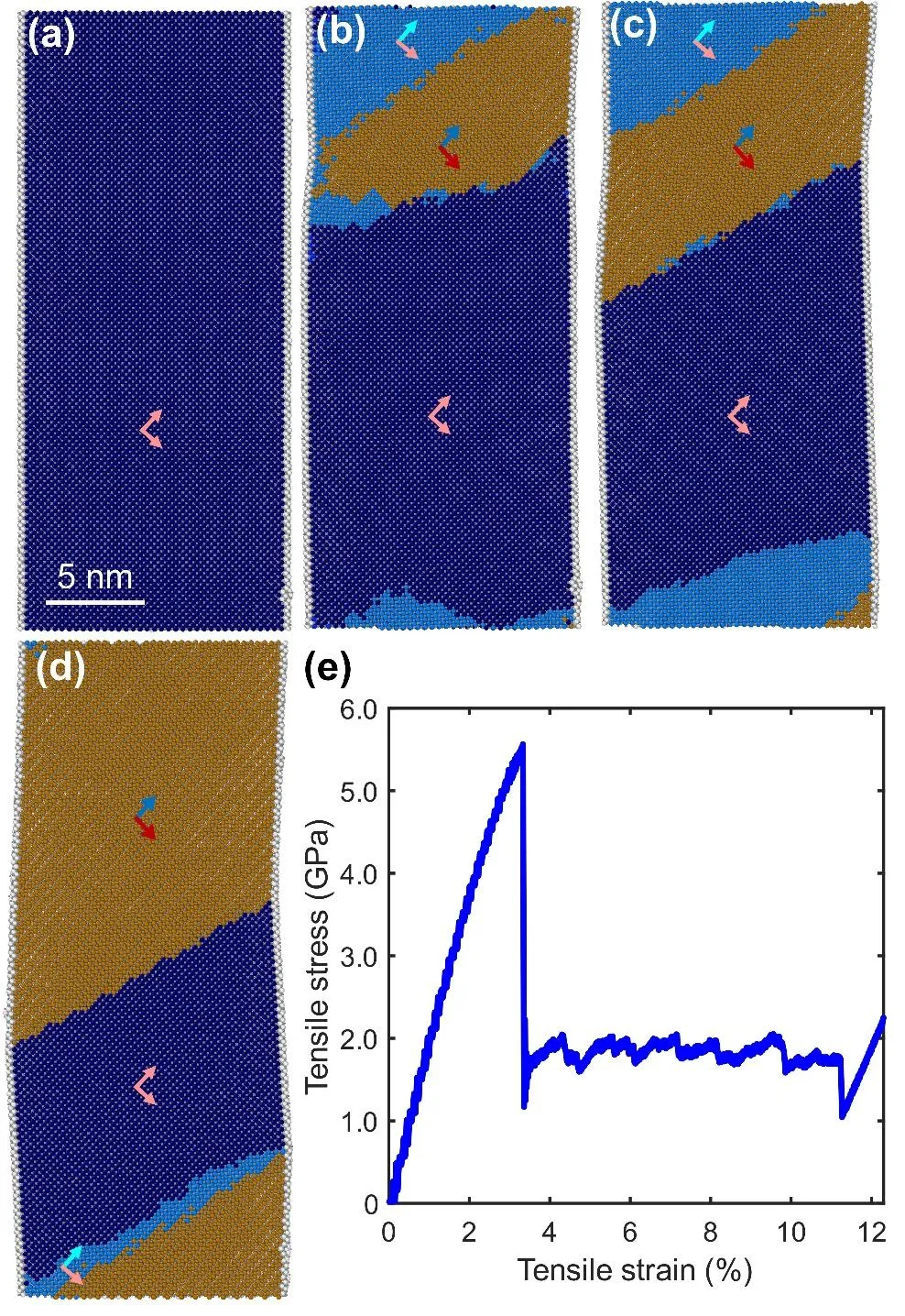
Figure6: Microstructural evolution process of a tetragonal ZrO₂ micropillar under ⟨110⟩ tensile simulation. Dark blue and light blue are the tetragonal structures before and after the ferroelastic transformation, respectively, and brown is the monoclinic phase formed by the phase transformation under the B correspondence.
Research Conclusions
The deep neural network potential developed in this study not only successfully predicts various key properties of zirconia ceramics but also reveals the intermediate state mechanism in the phase-transformation-induced plasticity effect, providing a new perspective for optimizing material properties in the future. At the same time, this work demonstrates the potential of the deep neural network potential in the study of complex material microstructures, especially in understanding the microstructure evolution of structural ceramic materials.
References
[1] X. M. Zeng, A. Lai, C. L. Gan, C. A. Schuh, Crystal orientation dependence of the stress-induced martensitic transformation in zirconia-based shape memory ceramics, Acta Mater. 116 (2016) 124–135.
[2] J.-Y. Zhang, G. Huynh, F.-Z. Dai, T. Albaret, S.-H. Zhang, S. Ogata, D. Rodney, A deep-neural network potential to study transformation-induced plasticity in zirconia, J. Eur. Ceram. Soc. 44 (2024) 4243–4254.