DeePTB | It supports strictly localized equivariant representation LCAO-quantum operators
In 2023, the AI for Science Institute, Beijing team introduced the v1 version of the DeePTB method, which was published on arXiv and joined the DeepModeling community. After nearly a year of rigorous peer review, it was officially published on August 8, 2024, in the international academic journal Nature Communications with the title "Deep learning tight-binding approach for large-scale electronic simulations at finite temperatures with ab initio accuracy" [1], DOI: 10.1038/s41467-024-51006-4.
The v1 version of DeePTB focuses on developing a deep learning-based method for constructing tight-binding (TB) model Hamiltonians. Based on the Slater-Koster TB parameterization, it builds first-principles equivalent electronic models using a minimal-basis set. By incorporating the localized chemical environment of atoms/bonds into the TB parameters, DeePTB achieves TB Hamiltonian predictions with near-DFT accuracy across a range of key material systems. By integrating with software like DeePMD-kit and TBPLaS, it enables the calculation and simulation of electronic structure properties and photoelectric responses in large-scale systems of up to millions of atoms in finite-temperature ensembles. This groundbreaking advancement has garnered widespread attention in the academic community and was ultimately published in Nature Communications. For more technical details on the DeePTB version, interested readers can refer to the DeePTB article in Nat Commun 15, 6772 (2024).
DeePTB v2: A Comprehensive Upgrade for LCAO Quantum Operators
During the review and publication process of the v1 version, the DeePTB project team did not remain idle. In July of this year, the team released DeePTB v2 [2], which involved a thorough restructuring and reorganization compared to v1. This new version integrates the deep learning representation of the TB Hamiltonian with E3 equivariant representations, including quantum operator matrices like the KS Hamiltonian and density matrix, within a unified software framework. Both the Slater-Koster TB and LCAO Kohn-Sham (KS) Hamiltonians are Hamiltonian operators represented under the Linear Combination of Atomic Orbitals (LCAO) framework. The key difference is that the Slater-Koster TB Hamiltonian is more constrained, particularly by the two-center approximation, and often uses fewer basis sets. The construction method used in v1 for the Slater-Koster TB Hamiltonian leverages the rotation of the Wigner-D matrix, enabling efficient parallel construction of the TB Hamiltonian matrix. As a result, the efficiency of v2 is significantly improved compared to v1.
In response to the high computational demands and parallelization challenges associated with the equivariant representation of quantum operators under the LCAO basis set, the DeePTB team implemented a solution that accelerates tensor operations using SO2. Additionally, to address the issue of the increasing receptive field with each iteration in MPNN networks, they designed a strictly localized equivariant message-passing model for representing single-particle operator matrices under the LCAO basis set, called SLEM (Strictly Localized Equivariant Message-passing). DeePTB v2 also flexibly supports the option to turn off the strict locality constraint, in which case the model is called LEM (Localized Equivariant Message-passing). The release of DeePTB v2 marks the evolution of DeePTB from a specialized TB model solution to a more general framework for accelerating first-principles calculations. Below, we introduce one of the core innovations of DeePTB v2, the SLEM model. For more details, please refer to the article: https://arxiv.org/abs/2407.06053.
Background and Principles of the SLEM Scheme
Predicting quantum operator matrices (such as Hamiltonians, overlap matrices, and density matrices) within the Density Functional Theory (DFT) framework is crucial for understanding material properties, but efficiently and scalably predicting these for large systems remains a challenge. Existing Message Passing Neural Network (MPNN) methods, though highly accurate on reported datasets, face limitations in parallelization, generalization, and scalability due to their iterative update mechanism, which expands the receptive field (i.e., the range over which nodes aggregate information). This challenge is even more pronounced in quantum operator prediction tasks, which involve handling high-dimensional variables. Therefore, a new strictly localized message-passing mechanism is needed to improve parallelization and scalability while maintaining high accuracy for handling large, complex systems.
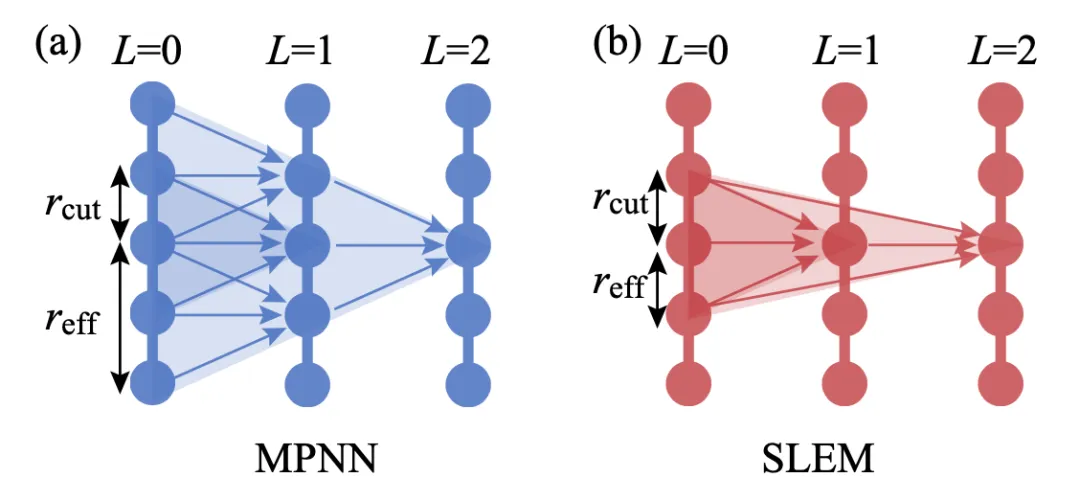
In traditional Message Passing Neural Networks (MPNNs), each round of node/edge feature updates depends on the updated features of nodes/edges from the previous layer. This update mechanism causes the receptive field to expand with the number of layers. As shown in Figure 1(a), after two layers of updates, the receptive field of a node expands twice from its initial neighborhood r_cut. This expansion makes each node/edge's output feature dependent on a vast input atomic/chemical bond environment, posing challenges for parallelization and scalability. In contrast, SLEM adopts a strictly localized feature update approach. "Strict locality" means that when updating node or edge features, it only relies on atomic environment information within a fixed range, which does not expand with network depth. As illustrated in Figure 1(b), for node updates, the update of the L-th layer node only depends on the features of the same node from the L-1 layer and the neighbor nodes from the L=0 layer. Through a clever message-passing mechanism design, the SLEM model consistently keeps the receptive field within a predefined local range while maintaining excellent expressive capability.
SLEM Model Architecture
The SLEM model utilizes equivariant neural networks to parametrize quantum operators such as Hamiltonians and density matrices. For the overlap integral matrix, SLEM leverages the strict two-center characteristic of orbital overlap integrals, employing Slater-Koster parameterization to achieve an invariant representation of the overlap integral matrix. Thanks to the unified framework of TB and E3 equivariant representation in the v2 version, SLEM significantly reduces the computational cost of fitting the overlap integral matrix.

This section focuses on the strictly localized equivariant representation scheme of the SLEM model. As shown in Figure 2, the SLEM model is primarily composed of the following parts:
Input Encoding: Encodes the physical and chemical information, such as atom types, coordination numbers, and distances, into hidden scalar features.
Feature Initialization: Initializes edge, hidden state, and node features using encoded scalars and spherical harmonics.
Feature Update Module: Iteratively updates the hidden state features, node features, and edge features through a series of strictly localized node/edge information update operations.
Quantum Operator Matrix Reconstruction: Reconstructs quantum operators such as Hamiltonians and density matrices using the updated node and edge features.
In summary, the SLEM model, through its strictly localized message-passing scheme, considers only the atomic environment within a fixed range when updating node and edge features, thereby avoiding the unlimited expansion of the receptive field. This design not only significantly improves data utilization efficiency and reduces computational costs but also removes technical barriers to parallelization, enabling efficient simulations on ultra-large systems. Additionally, for flexibility, DeePTB has also implemented a traditional MPNN-like scheme in the software that removes the strict locality constraint, instead using a learnable distance-weighted scheme to achieve equivalent locality, known as the LEM (Localized Equivariant Message-passing) model. Whether using SLEM or LEM, all equivariant models implemented in DeePTB v2 incorporate an efficient SO(2) convolution scheme, reducing the computational complexity of tensor products from (O(l^6)) to (O(l^3)), which provides strong support for handling systems with heavy elements (where DFT calculations require the inclusion of high angular momentum basis sets such as f and g orbitals).
In validation tests, DeePTB v2 demonstrated outstanding performance. The accuracy of Hamiltonian predictions reached sub-meV levels, and the prediction error for electron density and overlap matrices was on the order of (~1e-5), approaching the machine precision of single-precision floating-point numbers. Notably, due to DeePTB v2's ability to predict both Hamiltonians and overlap matrices simultaneously, the model operates independently of DFT software during inference. This greatly simplifies the DeePTB usage process, lowering the barrier for users. Furthermore, the clever Slater-Koster parameterization scheme allows the inclusion of overlap matrix training with minimal increase in model parameters and training time. Additionally, the strictly localized design of the SLEM model facilitates multi-GPU parallel inference and large-scale simulation applications in the future.
DeePTB Data Preprocessing Tool: dftio
During the development and application of DeePTB, the team realized that converting DFT output data into inputs for machine learning models is not an easy task, especially when dealing with different DFT software and training objectives. Users often need to overcome certain barriers, such as understanding the format of DFT data and the requirements of the model input, and then writing specific processing scripts for data preprocessing. To facilitate efficient reading, writing, and format conversion of electronic structure data from DFT software for users and the developer community, the DeePTB team initiated the dftio project. dftio aims to support the direct conversion of outputs from various DFT software into standard data formats required for electronic structure model training, as well as provide support for reading datasets in these standard formats. This significantly lowers the barrier to using electronic structure models like DeePTB and promotes the dissemination of data and methods. Moreover, with the convenience of a unified format, users can complete data conversion with just one command using dftio, without having to deal with complex data processing details, achieving a "what you see is what you get" experience. Additionally, dftio adopts a modular design, offering flexible interfaces, allowing users or developers to easily add support for new DFT software.
The Future of DeePTB: Collaborative Creation
Finally, while DeePTB has made significant progress and achievements, there are still many challenges to overcome on the path to a comprehensive revolution in first-principles calculations. To further enhance DeePTB’s performance and applicability, the DeePTB team is exploring more potential application scenarios with their partners. As an open-source project, the DeePTB team sincerely invites all interested colleagues to join. Whether you contribute valuable data resources, participate in model or software development, or provide suggestions for improvement, every contribution will help DeePTB reach higher goals. Various forms of collaboration are welcome, including but not limited to internships, visits, postdoctoral research, and other cooperative studies. We also encourage communication and discussion with the DeePTB team via GitHub Issues, email, or other means.
DeePTB is currently open-sourced in the DeepModeling community. We welcome you to use or join the project.
DeePTB Project Link: (https://github.com/deepmodeling/DeePTB)
The dftio project is in the process of applying to be hosted in the DeepModeling community, so stay tuned for more details.
Reference:
[1] Q. Gu, Z. Zhouyin, S. K. Pandey, P. Zhang, L. Zhang, and W. E, Deep Learning Tight-Binding Approach for Large-Scale Electronic Simulations at Finite Temperatures with Ab Initio Accuracy, Nat Commun 15, 6772 (2024).
[2] Z. Zhouyin, Z. Gan, S. K. Pandey, L. Zhang, and Q. Gu, Learning Local Equivariant Representations for Quantum Operators, arXiv:2407.06053.